RSA 공개키 암호화 알고리즘

RSA 공개키 암호화 알고리즘

RSA 암호화의 개념

RSA 암호화 방식은 1977년 3명의 연구자가 개발하였고 그들의 성을 따와서 이름을 만들었다.

RSA 공개키 암호화 알고리즘은 현대 암호화 알고리즘에서 많이 쓰이는 방식이고 안전성을 인정받아 인터넷 뱅킹에서 많이 쓰인다.

RSA 알고리즘의 핵심은 되돌리기 어려운 단방향 함수에 있다. 컴퓨터는 곱셈은 잘하지만 이미 곱해진 수를 인수분해 하는 것을 어려워 한다.

7654 곱하기 4567의 결과는 34,955,818이다. 이는 계산기로 손 쉽게 구할 수 있다.

그러나 34,955,818만을 가지고 어떤 두 수의 곱인지 알기는 어렵다.

RSA는 이 특성을 이용하고

브루트 포스 공격으로부터 나름 안전하다.

RSA 암호화 알고리즘은 비대칭키(공개키) 알고리즘 기반이다.

비대칭 암호화

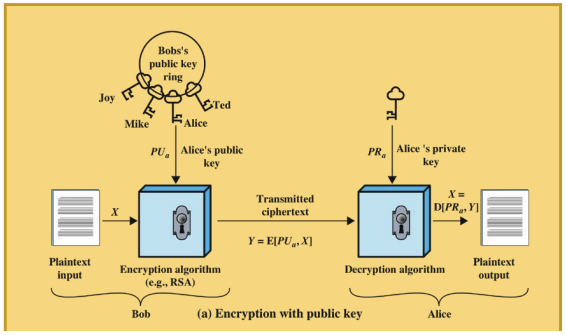
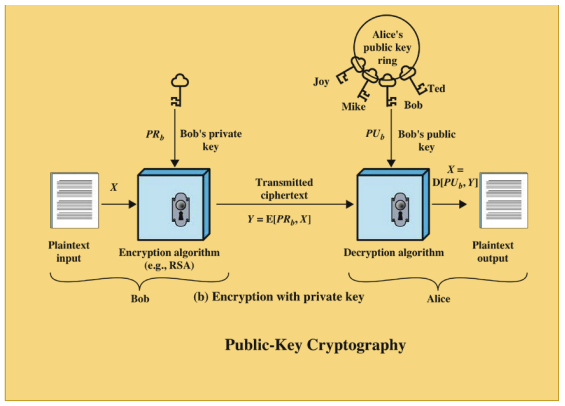
비대칭 암호화는 대칭키 암호화와 다르게 암호화와 복호화할 때 쓰이는 키가 서로 다르다.

RSA 과정

우선 공개키와 개인키 두 가지의 키를 만들어야 된다.

키 만들기

1. 서로 다른 임의의 두 개의 소수 p, q를 준비한다. 이 두 숫자는 클수록 암호화의 안정성이 높아진다.
2. p와 q를 곱한 값 N을 생성한다. (N = p*q)
3. p-1 , q-1과 각각 서로소인 정수 e를 구한다.
4. e·d를 (p-1)(q-1) 으로 나눈 나머지가 1이 되도록 하는 d를 찾는다.

여기서 N과 e 두 개가 공개키이며 d가 개인키가 된다.

3번의 e를 구하기 위해서는 오일러 파이 함수를 이용하는데

φ (n) = (p − 1) x (q − 1)

e는 1보다는 크지만 φ보다는 작고 서로소여야 한다. 주로 65,537이 RSA에 가장 많이 쓰이는 e이다.

암호화와 복호화 과정

평서문(M)를 암호문(C)으로 바꾸기 위해서는 다음 수식을 이용한다.

• C = M^e mod n

만약 전송하고자 하는 메시지가 숫자인 경우 M에 숫자를 그대로 넣고 텍스트인 경우 텍스트를 아스키 코드 등을 이용해 숫잘조 변환 후 대입한다.

암호문(C)를 다시 평서문(M)으로 바꾸는 수식은 아래와 같다.

• M = C^d mod n

예시

1. 두 소수 p와 q를 각각 11과 37으로 정하자.
2. N = 11 * 37 로 407 이다.
3. 10과 36과 동시에 서로소인 정수 e를 7로 정하자.
4. (7*d) % (10 *36) = 1 을 만족하는 d 값은 103이다.

정리하면

• p = 11 , q = 37
• N = 407
• e = 7
• d = 103

어떤 평서문 55를 암호화 해보자.

• C = 55^7 mod 407 = 198

암호문 198을 평서문으로 바꿔보자.

• M = 198^103 mod 407 = 55